Confidence Interval Calculator
Result
x = , CI
[, ]
You can be confident that the population mean (μ) falls between and .
Lower Bound:
Upper Bound:
Margin of Error (E):
When working with statistical data, understanding the range within which a population parameter is likely to fall is crucial. This is where a confidence interval comes into play, providing a statistical measure to estimate the range of values for an unknown parameter.
Our tool simplifies this process by allowing you to input your sample size, sample mean, and standard deviation to generate accurate confidence intervals at your desired confidence level. This is particularly useful for researchers, students, and professionals who need to draw conclusions from limited data sets.
By using our confidence interval calculator, you can quantify the uncertainty in your statistical estimates and make more informed decisions.
Key Takeaways
- Understand how to estimate the range of values for an unknown population parameter using a confidence interval.
- Learn how to use our confidence interval calculator to simplify statistical analysis.
- Discover the importance of confidence intervals in quantifying uncertainty in statistical estimates.
- Input your sample size, sample mean, and standard deviation to generate accurate confidence intervals.
- Make informed decisions by using confidence intervals in your statistical analysis.
Understanding Confidence Intervals
In statistical analysis, confidence intervals play a pivotal role in quantifying the uncertainty associated with sample estimates. By providing a range of values within which a population parameter is likely to lie, confidence intervals offer a measure of reliability for our estimates.
What Is a Confidence Interval?
A confidence interval is a statistical tool that estimates a population parameter based on a sample of data. It consists of a range of values, determined by the sample size, standard deviation, and confidence level. For instance, a 95% confidence interval for a population mean indicates that if we were to repeat the sampling process many times, 95% of the intervals constructed would contain the true population mean.
Importance in Statistical Analysis
Confidence intervals are crucial in statistical analysis because they provide a measure of the precision of our estimates. The width of a confidence interval is influenced by the sample size, confidence level, and standard deviation. A narrower interval indicates more precise estimates. Here are some key aspects:
- Confidence intervals help researchers make informed decisions by quantifying the uncertainty associated with statistical estimates.
- The sample size significantly affects the width of the confidence interval; larger samples result in narrower intervals.
- A higher confidence level results in a wider interval, indicating a trade-off between confidence and precision.
- Standard deviation impacts the interval width; lower standard deviation leads to narrower intervals.
How to Use Our Confidence Interval Calculator
Our Confidence Interval Calculator simplifies the process of determining the reliability of your sample data. By following a few straightforward steps, you can gain valuable insights into your data’s statistical significance.
Required Input Parameters
To use the calculator, you’ll need to input certain parameters from your sample data. These include the sample mean, standard deviation, and sample size. Ensuring that your data follows a normal distribution is crucial for accurate results. You’ll also need to choose a confidence level, typically set at 95%, although other levels like 90% or 99% can be used depending on your analysis requirements.
Interpreting Your Results
Once you’ve entered the necessary information, our calculator will provide you with the confidence interval. This range gives you an estimate of the population parameter you’re trying to measure. For instance, if you’re analyzing the average mass of bricks produced by a manufacturer, a 95% confidence interval of 2.85 kg to 3.15 kg means you can be 95% confident that the true average mass lies within this range, assuming a normal distribution of the data.
Common Applications
Our Confidence Interval Calculator has numerous practical applications across various fields, including quality control, medical research, opinion polling, and financial forecasting. For example, manufacturers use confidence intervals to ensure product specifications are met, while market researchers rely on them to estimate population parameters from sample data, such as consumer preferences or voting intentions.
Calculating Confidence Intervals
Calculating confidence intervals is a crucial step in statistical analysis to estimate the range within which a population parameter is likely to lie. This process involves several key components, including the sample mean, the standard deviation, the sample size, and the desired confidence level.
The Confidence Interval Formula
The formula to calculate confidence interval is given by: X̄ ± Z * (σ / √n), where X̄ is the sample mean, Z is the Z-score corresponding to the desired confidence level, σ is the population standard deviation, and n is the sample size. This formula is fundamental in determining the margin of error and thus the confidence interval.
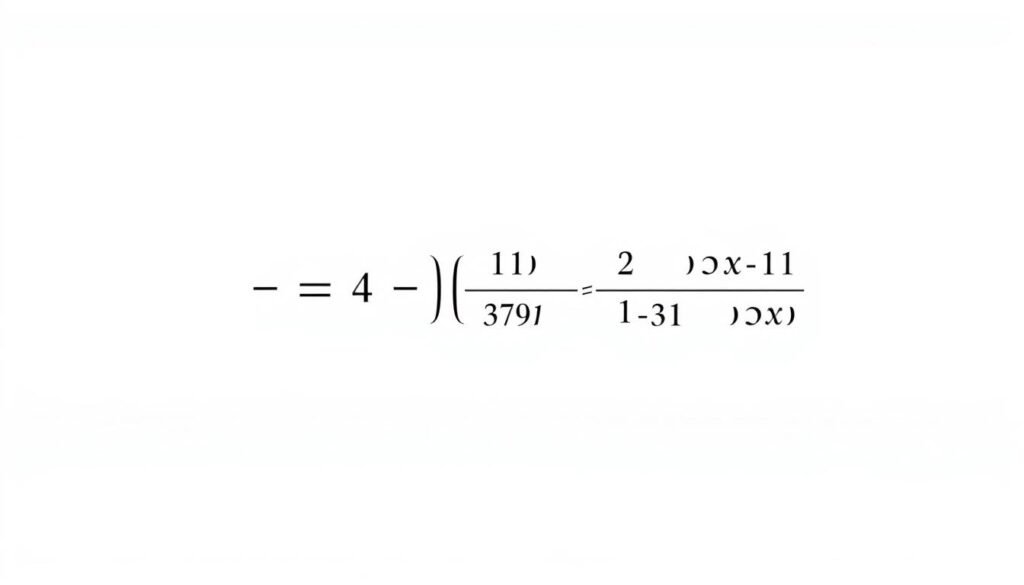
Z-Values for Different Confidence Levels
The Z-score is a critical value that corresponds to the desired confidence level. For instance, a 95% confidence level has a Z-score of 1.96. Other confidence levels have different Z-scores; for example, 90% confidence corresponds to a Z-score of 1.645, and 99% confidence corresponds to a Z-score of 2.576. Understanding these values is essential to calculate confidence intervals accurately.
Step-by-Step Calculation Example
Let’s consider an example to illustrate the step-by-step process of calculating a confidence interval. Suppose we have a sample with a mean (X̄) of 22.8, a population standard deviation (σ) of 2.7, and a sample size (n) of 100. For a 95% confidence level, the Z-score is 1.96. First, we calculate the standard error: 2.7 / √100 = 0.27. Then, we find the margin of error: 0.27 * 1.96 = 0.5292. Thus, the confidence interval is 22.8 ± 0.5292, resulting in an interval of [22.2708, 23.3292]. This range likely contains the true population mean with a 95% degree of certainty.
By following these steps and using the appropriate Z-score for the desired confidence level, one can easily calculate confidence interval for any sample data, providing a valuable estimate of the population parameter.
Conclusion
Ultimately, our confidence interval calculator simplifies complex statistical processes, making it easier to calculate confidence intervals with precision.
We’ve explored how this tool can be used with any arbitrary confidence level, handling both raw data and summary statistics to provide accurate results. Whether you’re a student, researcher, or professional, our calculator offers the reliability you need to make informed decisions.
By understanding the balance between precision and certainty that confidence intervals offer, you can better interpret your data. With our calculator, you can achieve the degree of certainty required for your statistical analysis.
FAQ
What is the purpose of using a confidence level in statistical analysis?
We use a confidence level to express the degree of certainty that our confidence interval contains the true population parameter. It represents the probability that the interval will contain the true value if we were to repeat the sampling process multiple times.
How do I determine the appropriate sample size for my study?
To determine the sample size, we consider factors such as the desired confidence level, the acceptable margin of error, and the population standard deviation. A larger sample size generally provides a more precise estimate of the population parameter.
What is the difference between a population standard deviation and a sample standard deviation?
The population standard deviation represents the variability of the entire population, while the sample standard deviation represents the variability of a subset of the population. We typically use the sample standard deviation when the population standard deviation is unknown.
Can I use a confidence interval calculator for non-normal distributions?
Our confidence interval calculator assumes a normal distribution. However, for non-normal distributions, we can use alternative methods or transformations to approximate normality. It’s essential to check the underlying distribution of our data before applying any statistical method.
How do I interpret the results of a confidence interval?
We interpret the confidence interval as a range of values within which the true population parameter is likely to lie. The width of the interval indicates the precision of our estimate, with narrower intervals indicating greater precision.
What is the relationship between the confidence level and the margin of error?
The confidence level and margin of error are inversely related. As we increase the confidence level, the margin of error also increases, resulting in a wider confidence interval. Conversely, decreasing the confidence level reduces the margin of error and narrows the interval.